od 시각화는 계속 진행 중인 시각화의 탐구 주제다.
최근 참여했던 프로젝트에서 지도상의 OD데이터 표현 방식에 있어 새로운 프로토타입을 개발해봤다.
OD데이터는 출발지와 목적지가 모두 여러개인 경우를 전제로 하지만, 이 프로토타입은 출발지나 목적지가 하나로 고정된 경우에 해당한다. 아래에서의 예시는 모두 출발지가 한 곳으로 고정되고 목적지가 다수인 일대다(多) 상황이다.
데이터는 2022년 전국 읍면동 인구이동 데이터를 사용했다. 통계청 MDIS에서 받아서 가공했다.
우선 그리고자 하는 결과물을 파워포인트로 간단하게 만들어봤다.
지도상의 이동 여러개를 한 번에 나타내고자 할 때 가장 어려운 부분은 '가까운 곳의 이동이 많다'는 점이다.
근거리와 원거리를 한 번에 표현해야 하는데 이동량까지 선의 굵기 등으로 표현하려고 한다면, 이동량이 많은 근거리 이동선이 겹쳐지면서 그림은 필연적으로 한 데 뭉쳐 '떡'이 되어 버린다.
그래서 아예 새로 시도해보는 프로토타입에서는 출발지를 중심점으로 하는 가상의 파이/도넛 그래프를 만들어 그 환형상에 이동량을 표시하는
전략을 취했다.
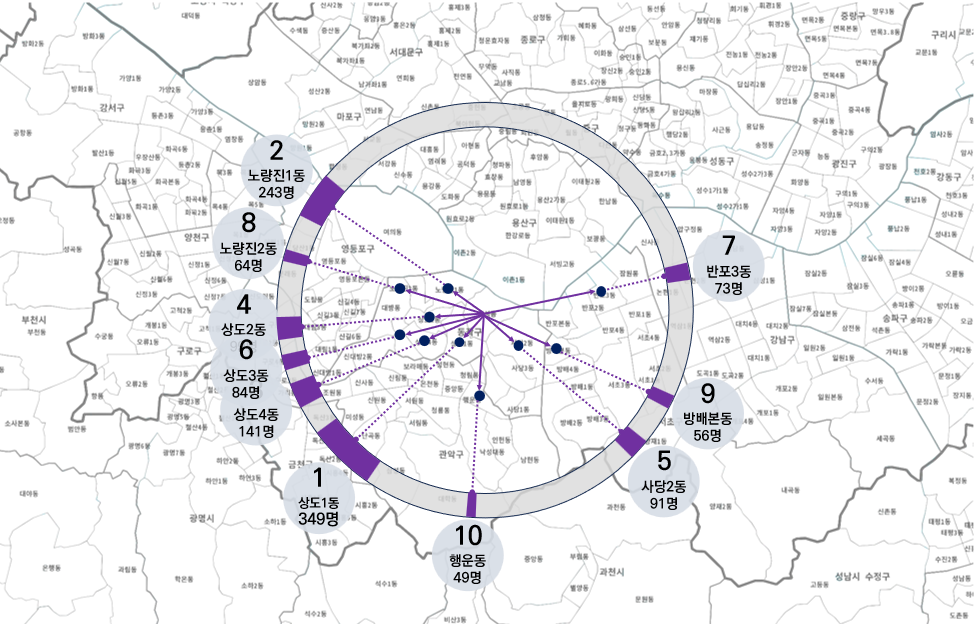
위의 예시는 흑석동에서 타 읍면동으로 전출한 경우 중 상위 10위까지를 표현하고 있다.
우선 도착지 읍면동 내부에 점을 하나씩 찍고, 출발지인 흑석동에서 실선 화살표로 연결했다.
그리고 그 중심점에서 환형까지 같은 진행 방향으로 점선을 그어 연장했다. 그렇게 닿은 지점에 이동량을 표시했다.
이동량은 흑석동에서 전출한 모든 인구 중 상대적 비율을 가리킨다.
만약 전체 전출량이 1000명이고, 1위 읍면동으로의 전출량이 100명이라면 그 읍면동의 연장선이 닿는 환형상에는 360도의 10% 인 36도만큼의 진하게 색으로 표시한다.
저렇게 규칙을 정해서 그려보면, 대략적인 이동량과 이동 방향이 한 눈에 들어온다.
흑석동의 상위 10위 전출 읍면동은 동쪽보다는 서쪽에 많다. 정확한 양의 차이는 계산해봐야 알 수 있지만, 대략 보아도 세배는 더 될 것 같다.
환형의 표현이 없는 경우를 보면 차이가 분명해진다.
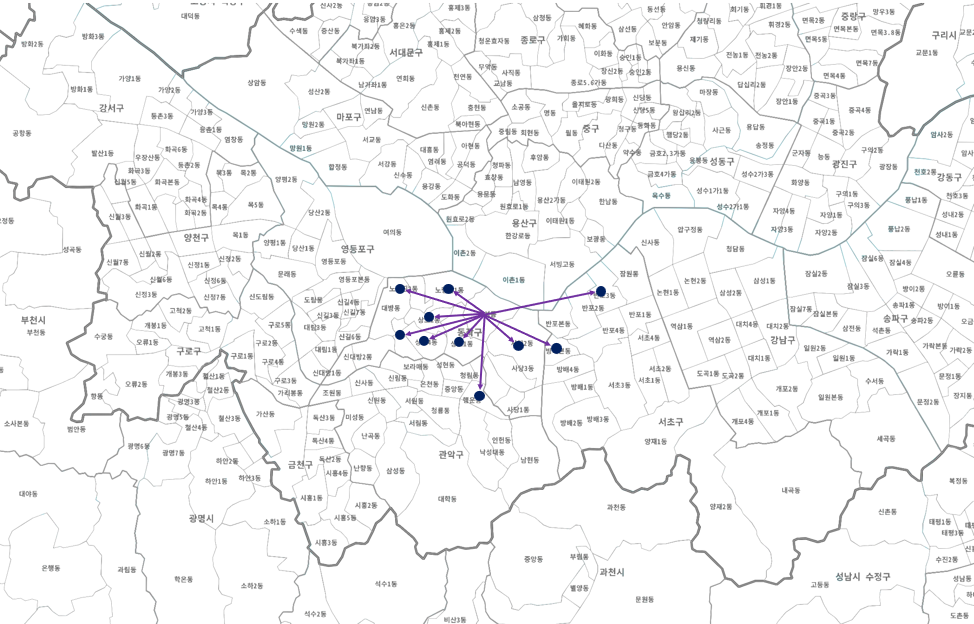
우선 동쪽과 서쪽의 차이가 한 눈에 들어오지 않는데, 여기에 선의 굵기를 표현한다고 생각해도 쉽게 식별될 것 같지는 않다.
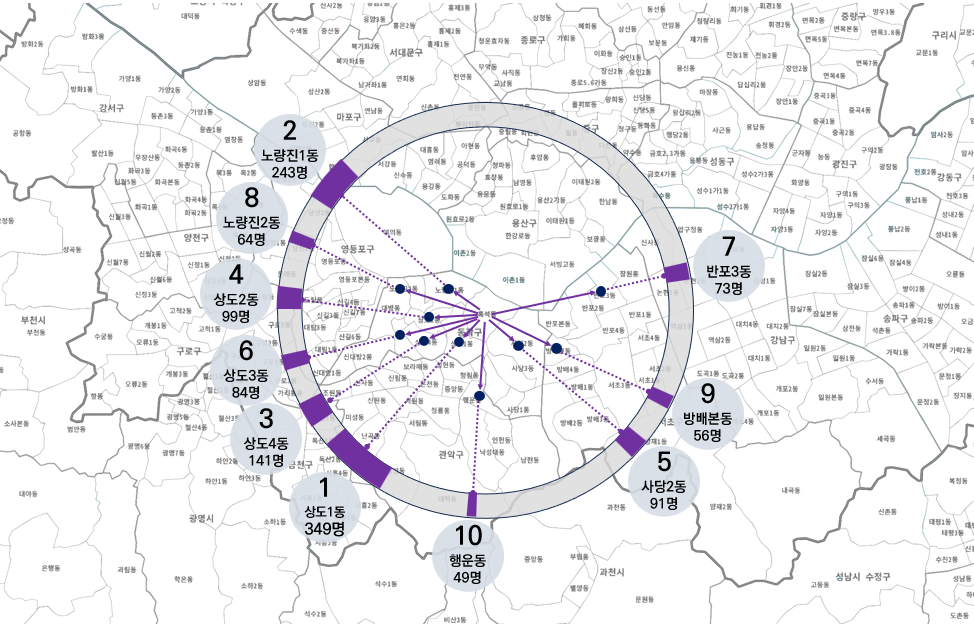
이 정도 검토를 거친 뒤 저렇게 구상한 안으로 반응형 프로토타입을 만들어보기로 했다.
우선 예상되는 문제는 방향이 같을 경우 선들이나 환형상의 색칠한 부분, 혹은 그 바깥의 글자들이 겹쳐보일 수 있다는 점이다.

구체적이 알고리즘은 나중에 생각하고, 일단 아래처럼 적절한 계산을 통해 여러 이동선의 중심을 유지한 채 적절한 간격으로 벌려보기로 했다.
그럼 이제 본격 만들어보자.
그냥 그리는건 그리 어렵지 않았다.
deck.gl로 읍면동 면에 색을 칠한 후 나머지는 svg 레이어를 위에 오버레이한 뒤, d3.js로 그렸다. viewState 변수에서 좌표값을 변경할 수 있는 project 함수등을 이용해서 지리 좌표와 스크린 상의 좌표들을 일치시켰다.
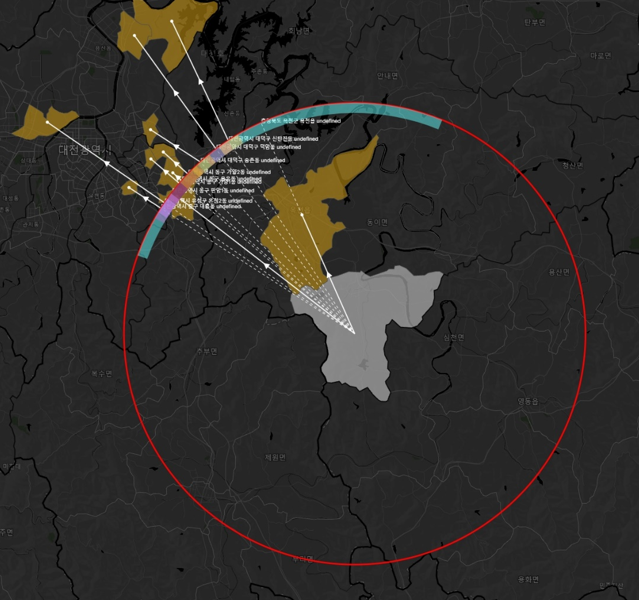
그리고 화면의 확대 축소 정도에 따라 10위 안의 지역들이 고리 바깥과 안쪽에 동시에 섞여서 위치할 경우들이 있었는데, 고리 바깥에 있을 경우에는 점선과 실선의 위치를 바꿔주었다. 즉, 고리 안쪽의 지역은 출발지~목적지를 실선, 목적지~고리까지를 점선으로 표현했는데, 고리 바깥의 경우에는 출발지~고리까지를 점선으로, 고리~목적지까지를 실선으로 표현했다.
'왜'라고 정확히 설명하기는 어려운데, 그렇게 해야 좀 더 직관적으로 잘 보였다. 출발지에서 점선으로 출발하는 상황만 보아도 상위 10위에 목적지가 먼 곳들이 있다는 정보가 제공되는 셈이다.
위의 그림은 이 규칙을 잘 보여준다. 아직 겹침 문제는 해결되지 않은 경우다.
겹침 문제를 해결하려고 하면서 예상치 못한 경우들이 생각보다 많이 등장했다.
주로 상위 10위의 이동 방향들이 한 곳으로 몰릴 경우에 발생했는데,
간격을 벌리면 이동선들이 심하게 꺾여서 환형에 새겨지는 이동량의 표현 위치가 원래 방향에서 많이 꺾이거나 순서들이 뒤죽박죽으로 보이는 경우가 있었다.
아래 그림은 간격을 벌리는 단계까지만 진행했는데 바로 위에서 지적한 문제들을 잘 보여준다.
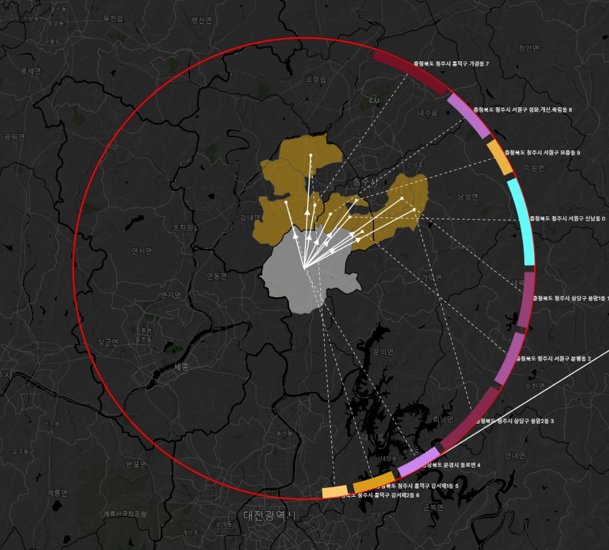
이동의 방향성이 주로 북쪽인데 정렬 및 재정비된 결과는 동쪽으로 치우쳐 있다.
그리고 점선들이 서로 교차할 경우 정리되지 않은 것처럼 보인다.
그래서 우선 재조정 과정에서 이동량에 가중치를 두어 전체 군집의 중심이 유지되도록 했다. 그럼에도 불구하고 예상치 못한 경우들이 또 등장해서 몇 가지 규칙들을 더 추가했다.
조정하는 부분의 코드를 옮겨보자면 아래와 같다.
//겹친 위치들을 적절히 조정한다.
function adjustRatioBarLocation(
orixy_scr: any, //출발 중심점 화면 좌표
top10: any, //top10 데이터가 들어있는 객체의 배열
outerRadius: number //출발중심점에서 환형까지의 거리
) {
//console.log("top10:", top10);
//데이터 준비
prepareData();
//겹치는 요소들을 펼치면서 조정한다.
rearrangeOverlap();
//교차하는 선들을 스왑 형식으로 순차적으로 풀어낸다.
unravelLines();
return;
//이어지는 함수 안의 함수들
//function prepareData() {...}
//function rearrangeOverlap() {...}
//function unravelLines() {...}
}
위에서 보듯 세 단계로 나눠봤다.
function prepareData() {
//top10의 순서대로 인덱스를 부여한다.
top10.forEach((d: any, i: number) => {
d.rank = i;
});
top10.forEach((d: any, i: number) => {
const distToDesxy = Math.sqrt(
(orixy_scr.x - d.desxy_scr.x) ** 2 + (orixy_scr.y - d.desxy_scr.y) ** 2
);
if (distToDesxy <= outerRadius) {
d.isInner = true;
} else {
d.isInner = false;
}
});
//top에 desExtendedArr와 normalVector 각도를 추가한다.
top10.forEach((d: any, i: number) => {
d.angle = Math.atan2(
d.desxy_scr_outer.y - orixy_scr.y,
d.desxy_scr_outer.x - orixy_scr.x
);
});
}
우선 준비단계인 1단계에서는 바깥쪽 지역과 안쪽 지역을 구분하면서 계산에 쓰일 각도 등의 변수들을 미리 계산했다.
핵심은 2단계와 3단계다.
2단계 함수는 아래와 같다. 설명은 코드 안의 주석으로 대신한다.
function rearrangeOverlap() {
//top을 angle로 정렬한다.
top10.sort((a: any, b: any) => a.angle - b.angle);
const buffer = 0.03;
const moveLimit = 0.03;
//top을 순회하면서 이전, 이후 요소와의 각도 차이를 구한다.
//ratioBar의 폭을 구한다. 폭은 angle 끝점에서 양쪽으로 360도 중 차지하는 비율의 절반만큼씩이다.
//ratioBar가 이전, 이후 요소와 겹치지 않도록 조정한다.
//이전 요소와 겹치면 이전 요소와 지금 요소가 서로 반대 방향으로 조금씩 이동한다.
//이후 요소와 겹치면 이후 요소와 지금 요소가 서로 반대 방향으로 조금씩 이동한다.
//이동하는 정도는 ratio에 반비례한다. 즉, ratio가 클수록 조금 이동하고 작을수록 많이 이동한다.
//겹치는 만큼 모두 이동하지 말고, 이동은 1도 이하로 제한한다.
//마지막 요소의 경우에는 처음 요소와도 비교한다. 원으로 상정하고 있기 때문이다.
//이 비교를 800회 반복한다. 물론 조정할 내용이 없으면 중간에 종료한다.
for (let i = 0; i < 800; i++) {
let moveCnt = 0;
for (let prev = 0; prev < top10.length; prev++) {
for (let next = prev + 1; next < top10.length; next++) {
const angleDiff = angleDifference(
top10[prev].angle,
top10[next].angle
);
const prevRatio = top10[prev].ratio;
const nextRatio = top10[next].ratio;
//두 각 중 180도 이내의 각도 차이 기준으로 prevAngle이 시계방향쪽에 있는지 확인한다.
let moveDirection = 1;
const isPrevCW =
Math.abs(top10[prev].angle - top10[next].angle) < Math.PI;
if (isPrevCW) moveDirection = -1;
const prevWidthHalf = prevRatio * Math.PI;
const nextWidthHalf = nextRatio * Math.PI;
const overlap =
prevWidthHalf + nextWidthHalf + buffer - Math.abs(angleDiff);
if (overlap > 0) {
let move = Math.min(moveLimit, Math.abs(overlap));
let weight_next =
top10[prev].ratio / (top10[prev].ratio + top10[next].ratio);
let weight_prev =
top10[next].ratio / (top10[prev].ratio + top10[next].ratio);
top10[prev].angle += moveDirection * move * weight_prev;
top10[next].angle -= moveDirection * move * weight_next;
if (move > 0.001) moveCnt++;
//console.log("weight_prev+weight_this:", weight_prev, weight_this);
}
}
}
if (moveCnt === 0) {
//console.log("loop:", i);
break;
}
}
//각 요소의 최종 위치를 계산하여 업데이트합니다.
top10.forEach((d: any) => {
d.adjustedOuter = {
x: orixy_scr.x + outerRadius * Math.cos(d.angle),
y: orixy_scr.y + outerRadius * Math.sin(d.angle),
};
});
}
3단계는 겹치는 선들을 조정하는 단계다.
점선이 교차하지 않을때까지 서로 swap해가는 방식, 즉 일종의 정렬 알고리즘을 차용해서 만들었다.
function unravelLines() {
top10.sort((a: any, b: any) => a.angle - b.angle);
//console.log("top10:", top10);
let crossCnt = 1;
//점선이 교차하는지 검증해서 교차하면 서로 스왑한다.
while (crossCnt > 0) {
//console.log("crossCnt:", crossCnt);
crossCnt = 0;
for (let j = 0; j < top10.length; j++) {
const p0 = top10[j];
const p1 = j == top10.length - 1 ? top10[0] : top10[j + 1];
const line0_ori = p0.isInner ? p0.desxy_scr : orixy_scr;
const line0_des = p0.adjustedOuter;
const line1_ori = p1.isInner ? p1.desxy_scr : orixy_scr;
const line1_des = p1.adjustedOuter;
//line0과 line1 선분이 교차하는지 검증한다.
const isCross = checkLineCross(
line0_ori,
line0_des,
line1_ori,
line1_des
);
//console.log("i,j:", p0.index, p1.index, isCross);
if (isCross) {
//console.log("cross:", p0.index, p1.index);
//교차하면 서로 스왑한다.
swapAngle(p0, p1);
crossCnt++;
p0.adjustedOuter = {
x: orixy_scr.x + outerRadius * Math.cos(p0.angle),
y: orixy_scr.y + outerRadius * Math.sin(p0.angle),
};
p1.adjustedOuter = {
x: orixy_scr.x + outerRadius * Math.cos(p1.angle),
y: orixy_scr.y + outerRadius * Math.sin(p1.angle),
};
//매번 정렬하지 않으면 어디선가 꼬인다.
top10.sort((a: any, b: any) => a.angle - b.angle);
}
}
}
}
위의 진행에서 사용되는 util 함수들은 아래와 같다.
computational geometry 영역의 기본기들을 섞었다고 보면 된다.
예전에는 구현할때마다 부호 때문에 좀 헷갈렸었는데, 일부는 이런 기본 함수들을 훌륭하게 빠른 속도로 구현하는 chatGPT에게 시킨 뒤 검증하는 식으로 만들었다.
function angleDifference(angle1: number, angle2: number) {
let diff = angle2 - angle1;
while (diff > Math.PI) {
diff -= 2 * Math.PI;
}
while (diff < -Math.PI) {
diff += 2 * Math.PI;
}
return diff;
}
function isAngle0CWFunc(angle0: number, angle1: number) {
// 두 각도의 차이를 구합니다.
let diff = angle1 - angle0;
// 차이를 -π와 π 사이의 값으로 만듭니다.
while (diff > Math.PI) {
diff -= 2 * Math.PI;
}
while (diff < -Math.PI) {
diff += 2 * Math.PI;
}
return diff > 0 ? false : true;
}
//각 요소의 angle위치에서 ratio의 절반만큼 angle 바깥쪽으로 offset한다.
//각각 바깥쪽으로 offset한 두 angle의 중점을 구한다.
//그 중점을 기준으로 angle을 점대칭해서 바꾼다.
function swapAngle(p0: any, p1: any) {
const angle0 = p0.angle;
const angle1 = p1.angle;
const ratio0 = p0.ratio;
const ratio1 = p1.ratio;
const offset0 = ratio0 * Math.PI;
const offset1 = ratio1 * Math.PI;
//angle0이 angle1보다 시계방향에 있으면 angle0에서는 offset을 더하고,
//angle1에서는 offset을 뺀다.
const isAngle0CW = isAngle0CWFunc(angle0, angle1);
const angle0_outer = isAngle0CW ? angle0 + offset0 : angle0 - offset0;
const angle1_outer = isAngle0CW ? angle1 - offset1 : angle1 + offset1;
if (isAngle0CW) console.log("isAngle0CW:", angle0, angle1);
const angle1_new = isAngle0CW
? angle0_outer - offset1
: angle0_outer + offset1;
const angle0_new = isAngle0CW
? angle1_outer + offset0
: angle1_outer - offset0;
p0.angle = angle0_new;
p1.angle = angle1_new;
}
function checkLineCross(p0: any, p1: any, p2: any, p3: any) {
const ccw = (p0: any, p1: any, p2: any) => {
return (p2.y - p0.y) * (p1.x - p0.x) > (p1.y - p0.y) * (p2.x - p0.x);
};
return (
ccw(p0, p2, p3) !== ccw(p1, p2, p3) && ccw(p0, p1, p2) !== ccw(p0, p1, p3)
);
}
기하학을 좋아한다면 데이터 시각화 중 어떤 부분들에서는 분명한 장점이 된다.
대부분 추상화된 점,선,면으로 구현하기 때문이다.
클라이언트에게 '대상이 무엇이든 논리적으로 설명할 수 있으면 그릴 수 있다'고 말하곤 하는데, 그 논리적 설명을 구현하려면 computational geometry는 필수적으로 공부해야 하는 영역이다.
이제 색상들을 좀 더 가다듬어서 정리해봤다.
처음에 ppt로 그렸던 흑석동의 사례다.
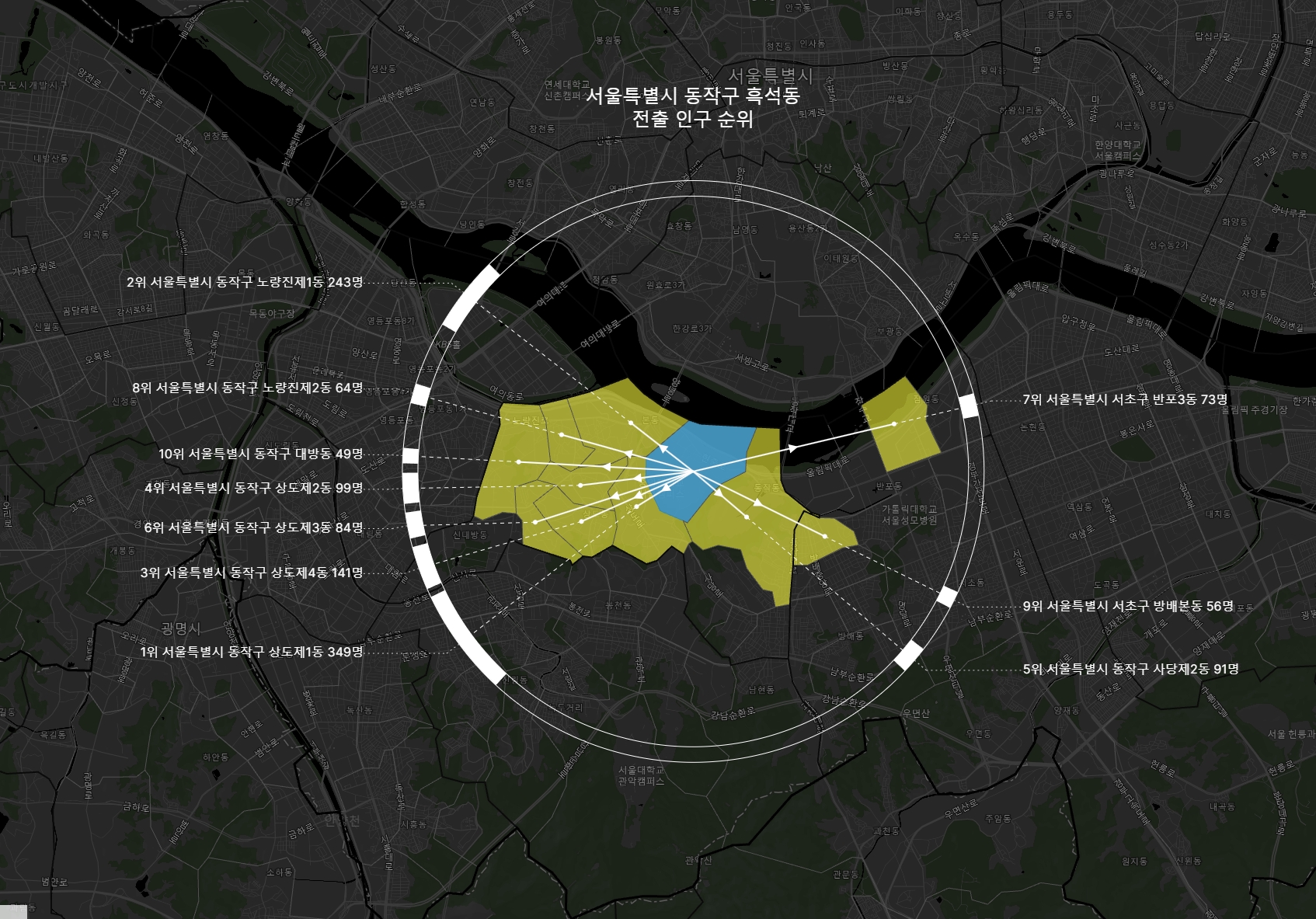
예시로 그려볼 때는 몰랐는데, 이 경우는 굉장히 얌전한 경우였다.
전체 원을 표현하는 선은 불필요한 것 같기도 해서 지우고 색상을 좀 바꿔봤다.
이동량과 대략적인 이동 방향이 한 눈에 좀 더 잘 들어온다.
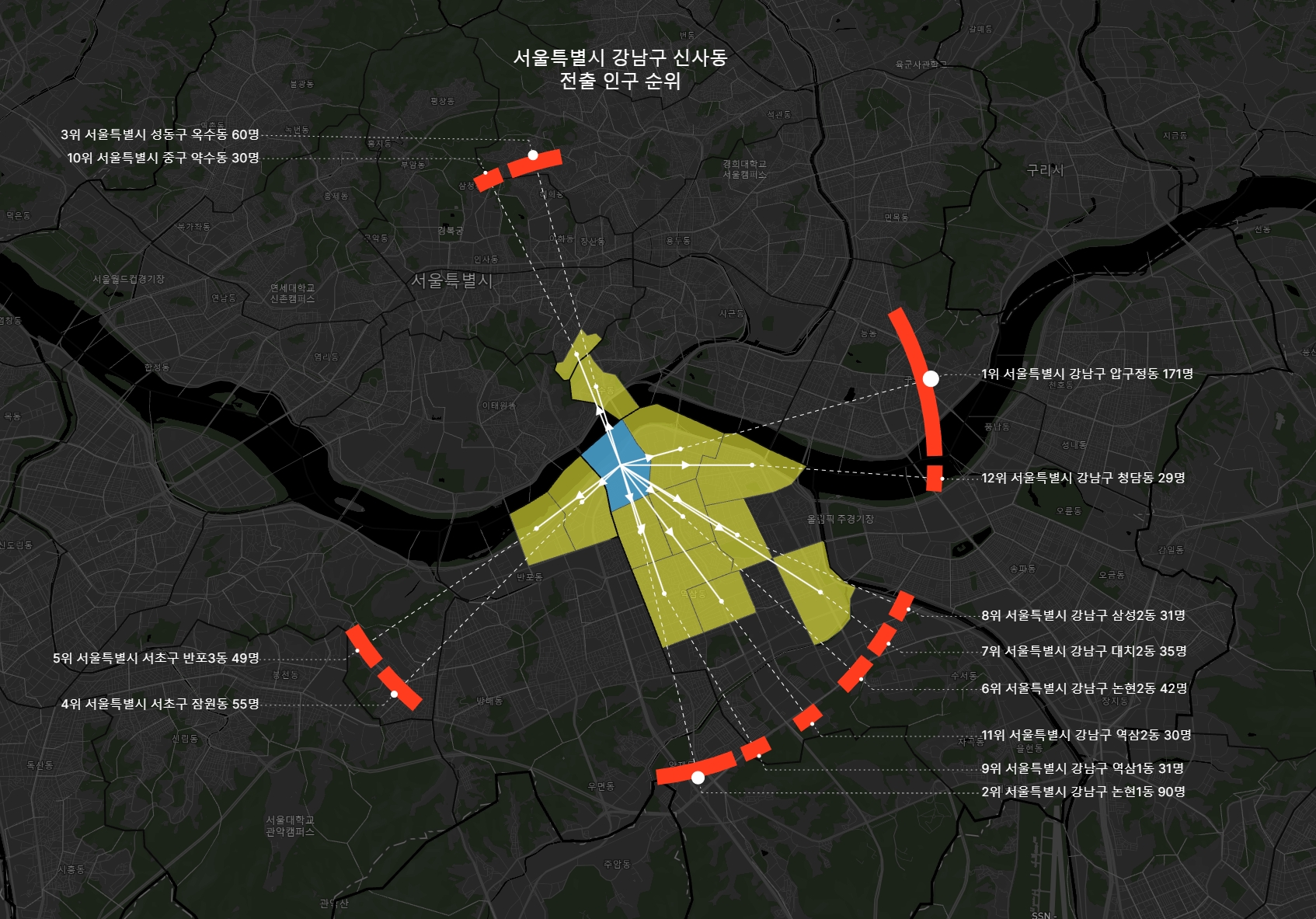
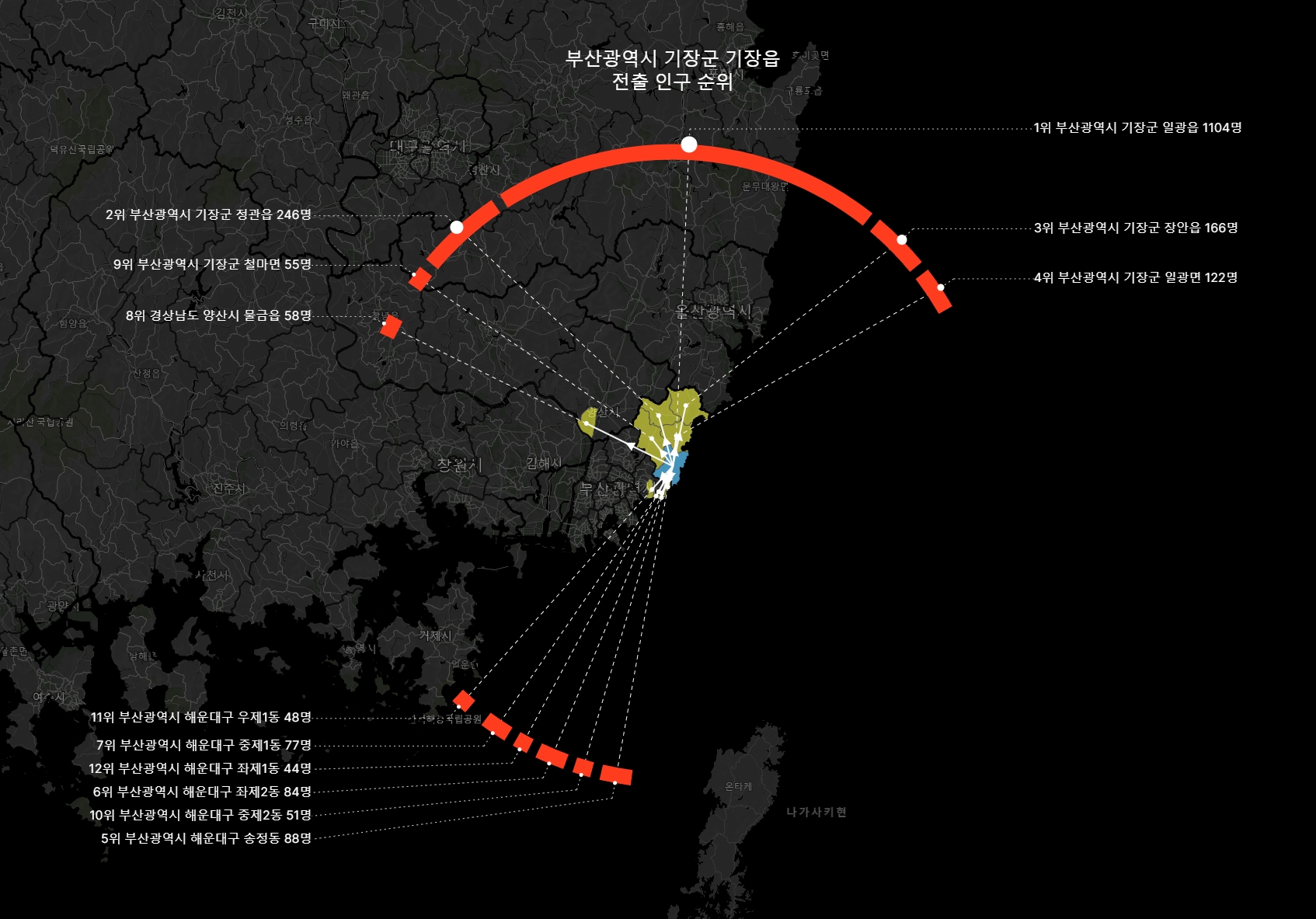
아래 두 장의 그림은 같은 지역이 zoom에 따라 어떻게 다르게 표현되는지 보여준다.
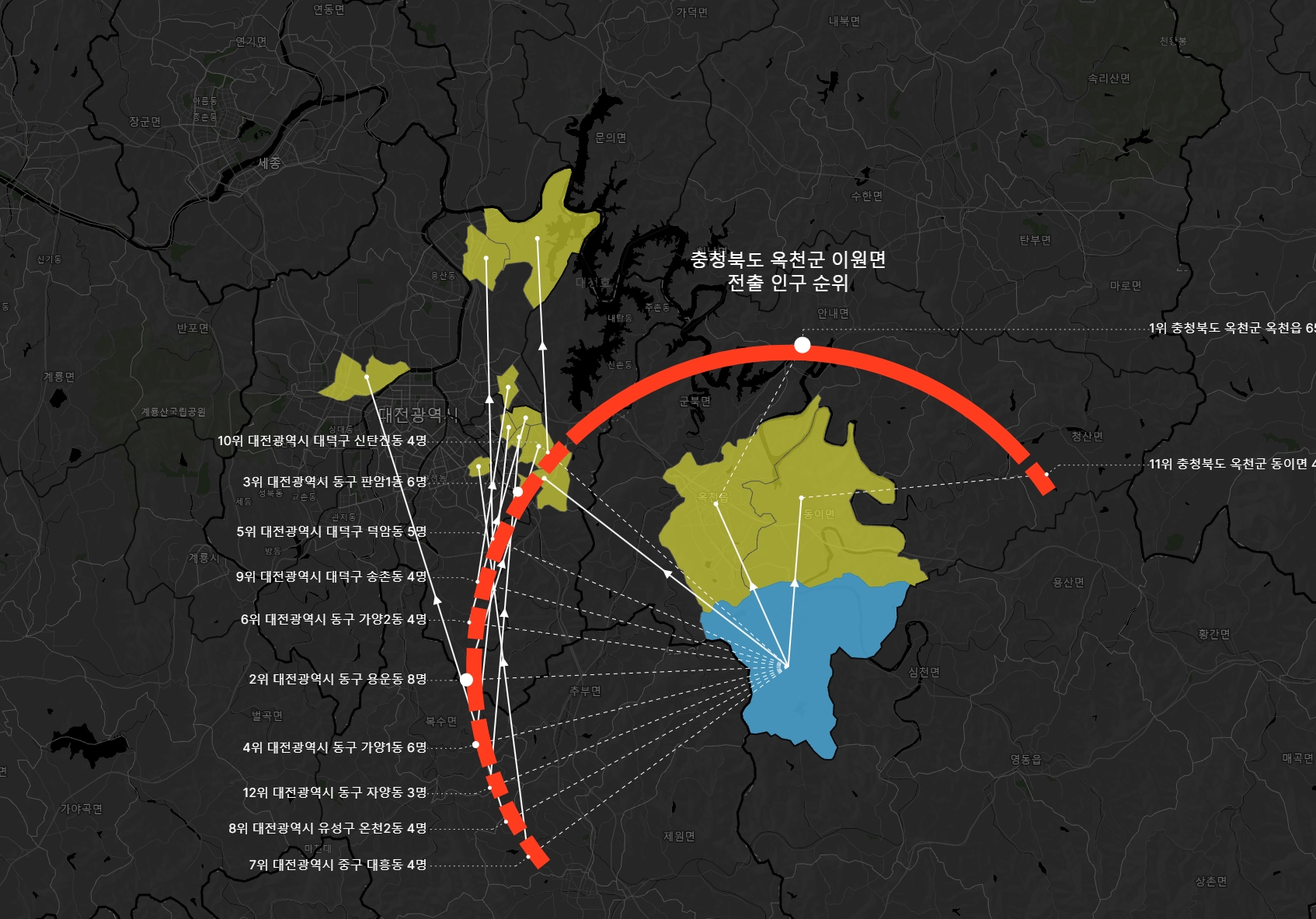
zoom out 하면서 고리 안쪽으로 들어온 부분들은 점선과 실선이 뒤바뀐다.
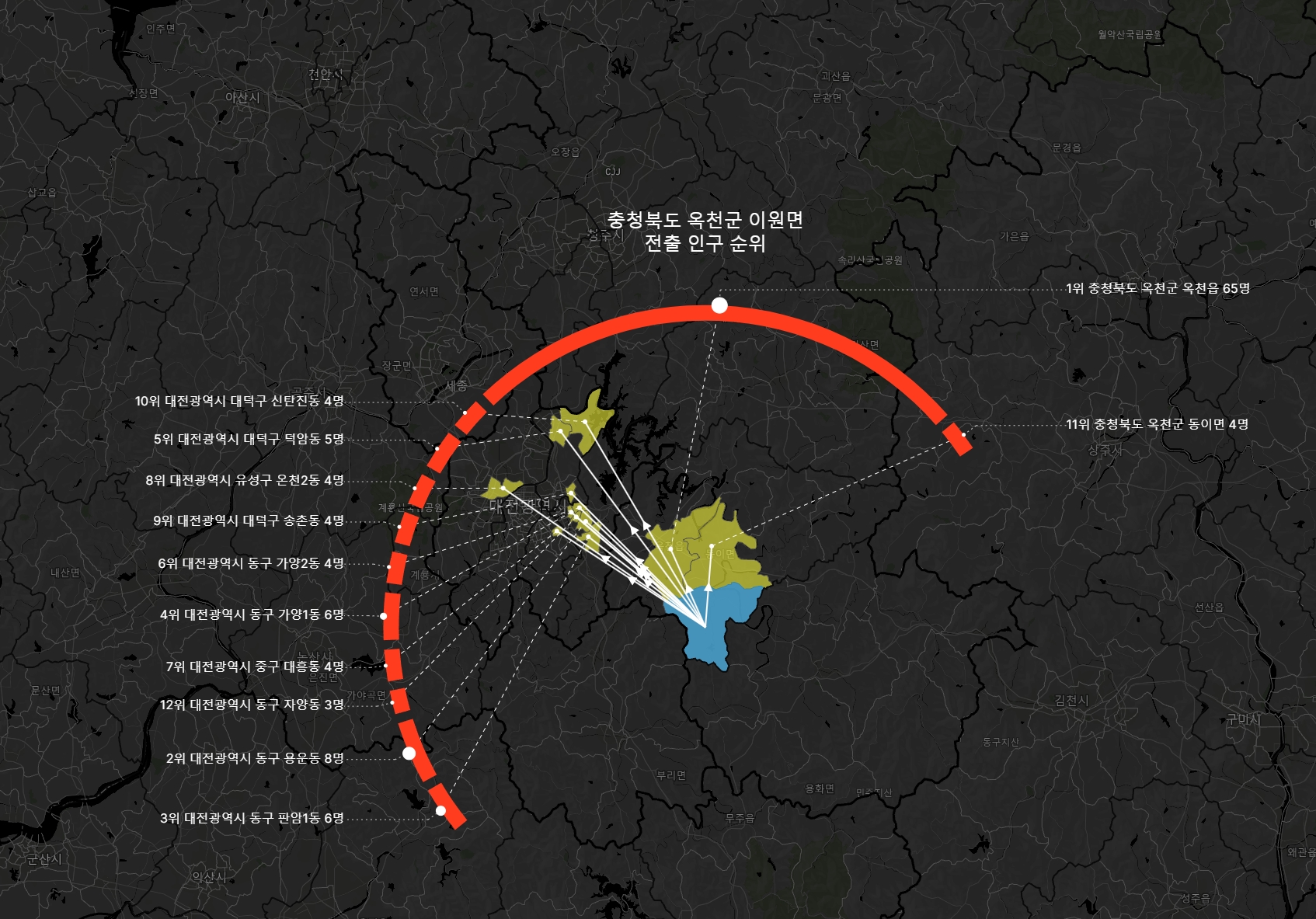
옥천군 이원면 같은 경우 옥천읍으로 65명 이동했는데, 2위~10위까지 모두 합한 것과 비슷한 정도다. 1위의 전출량 비중이 상당함을 쉽게 인지할 수 있다.
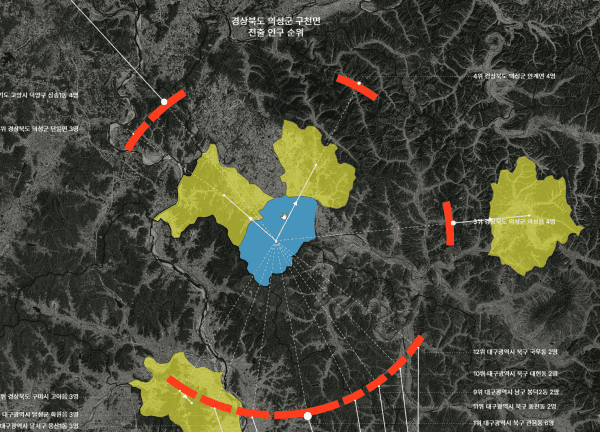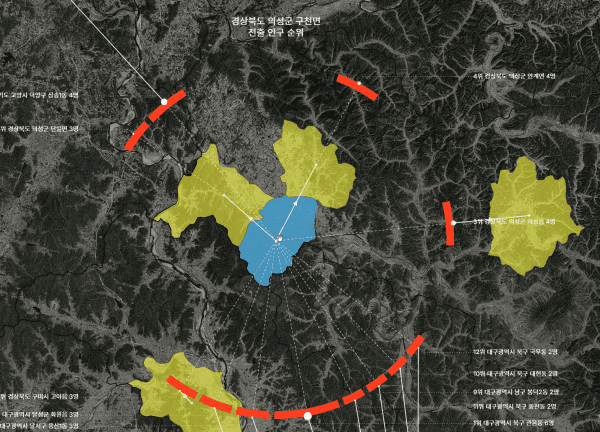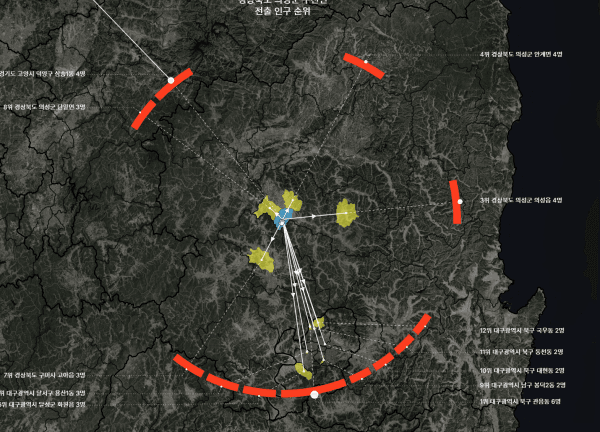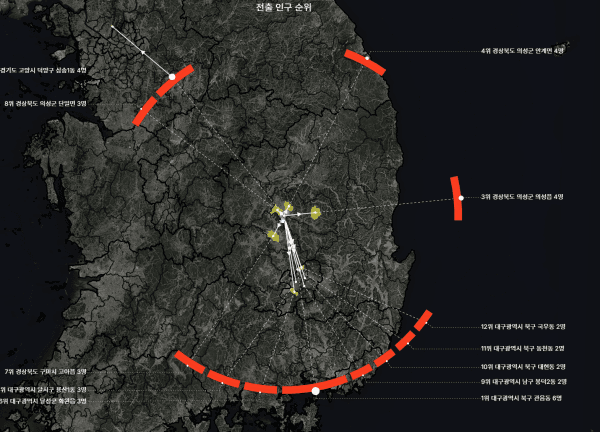
영덕군 영덕읍
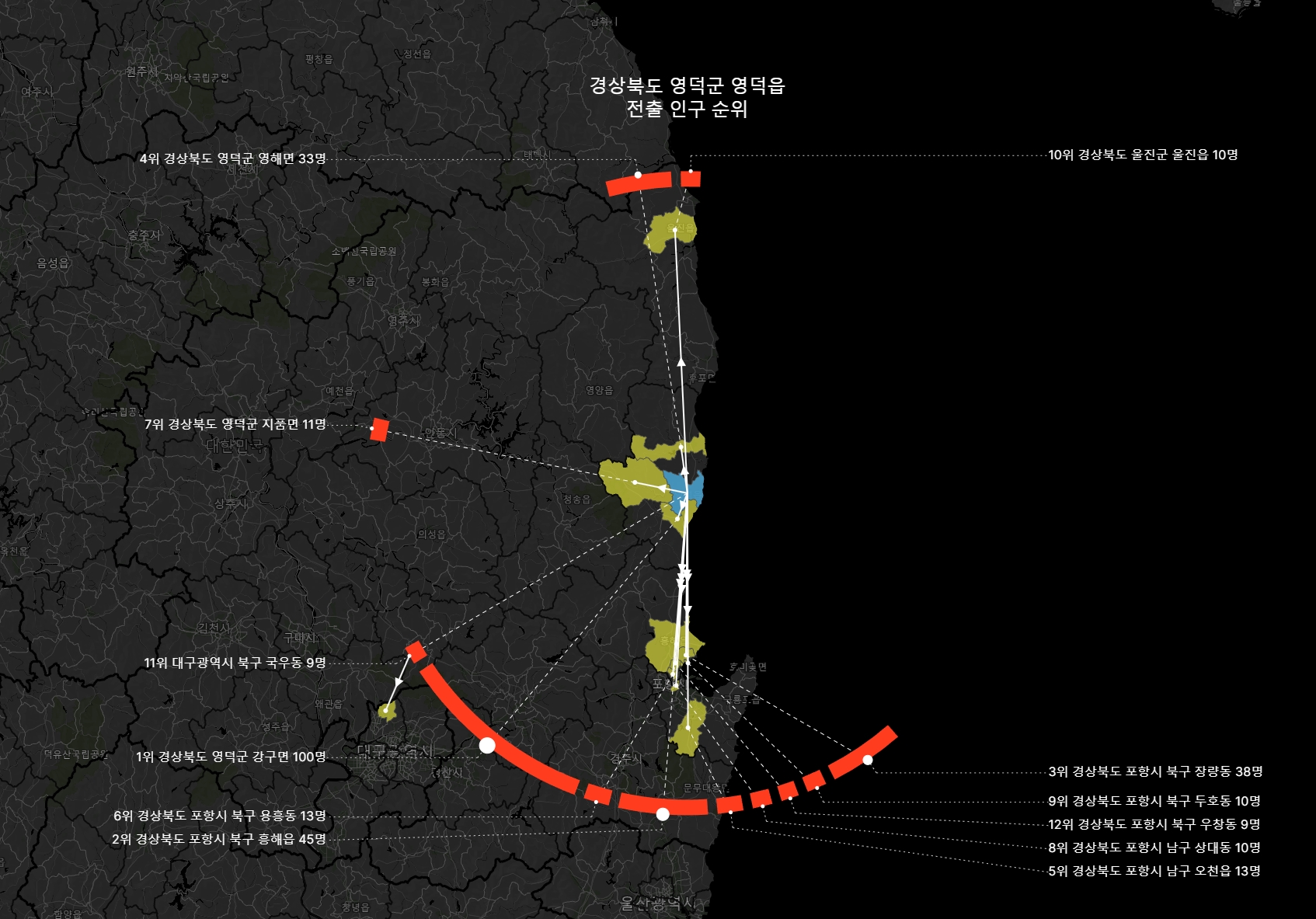
지역만 칠해놓고 보면 어디로 얼마만큼 이동했는지 알기 어렵지만, 환형의 표현을 덧대어보니 남측으로의 이동이 대다수임이 한 눈에 들어온다.
지도가 축소 상태일때도 이동량과 이동 방향을 쉽게 알아볼 수 있다.
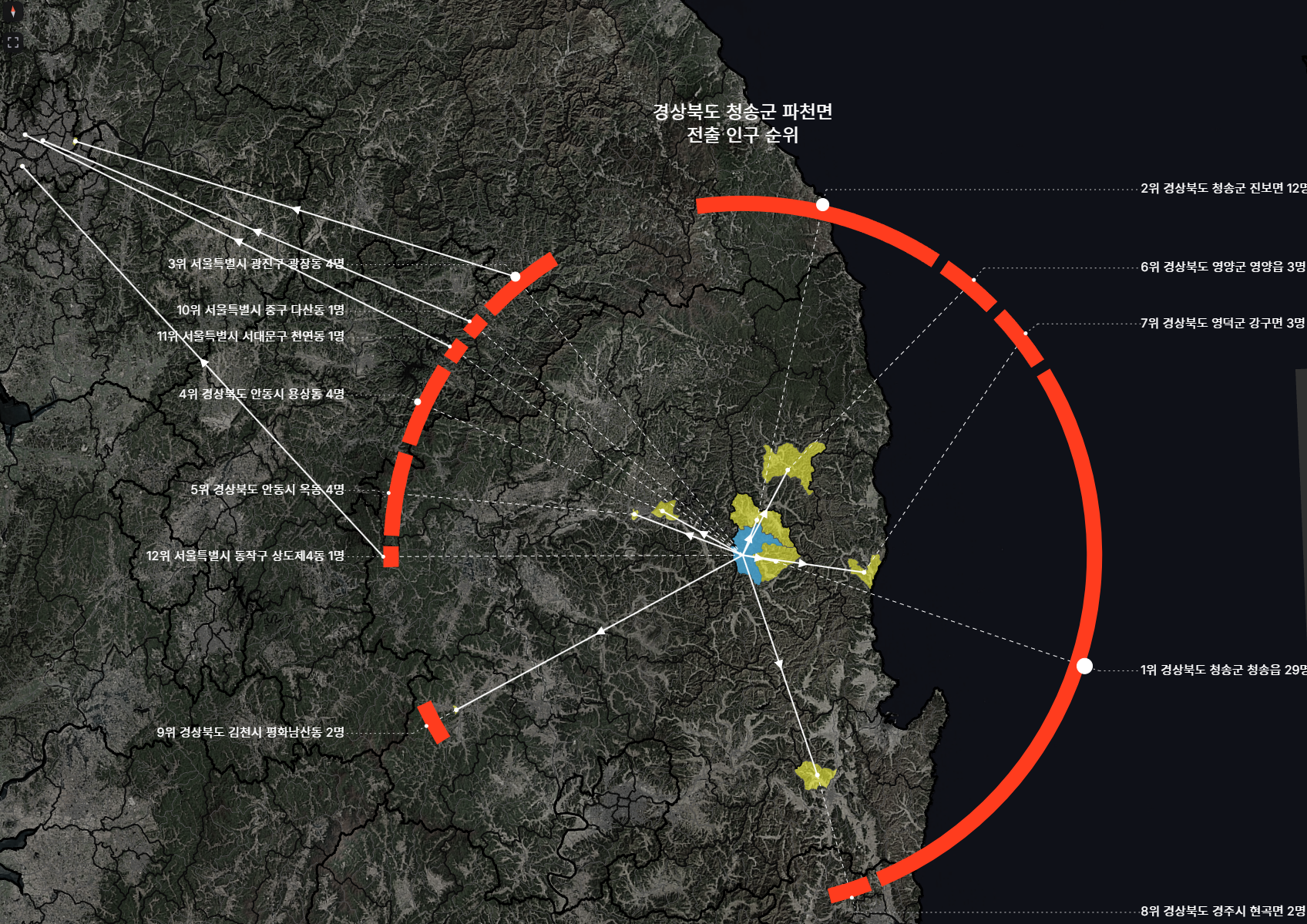
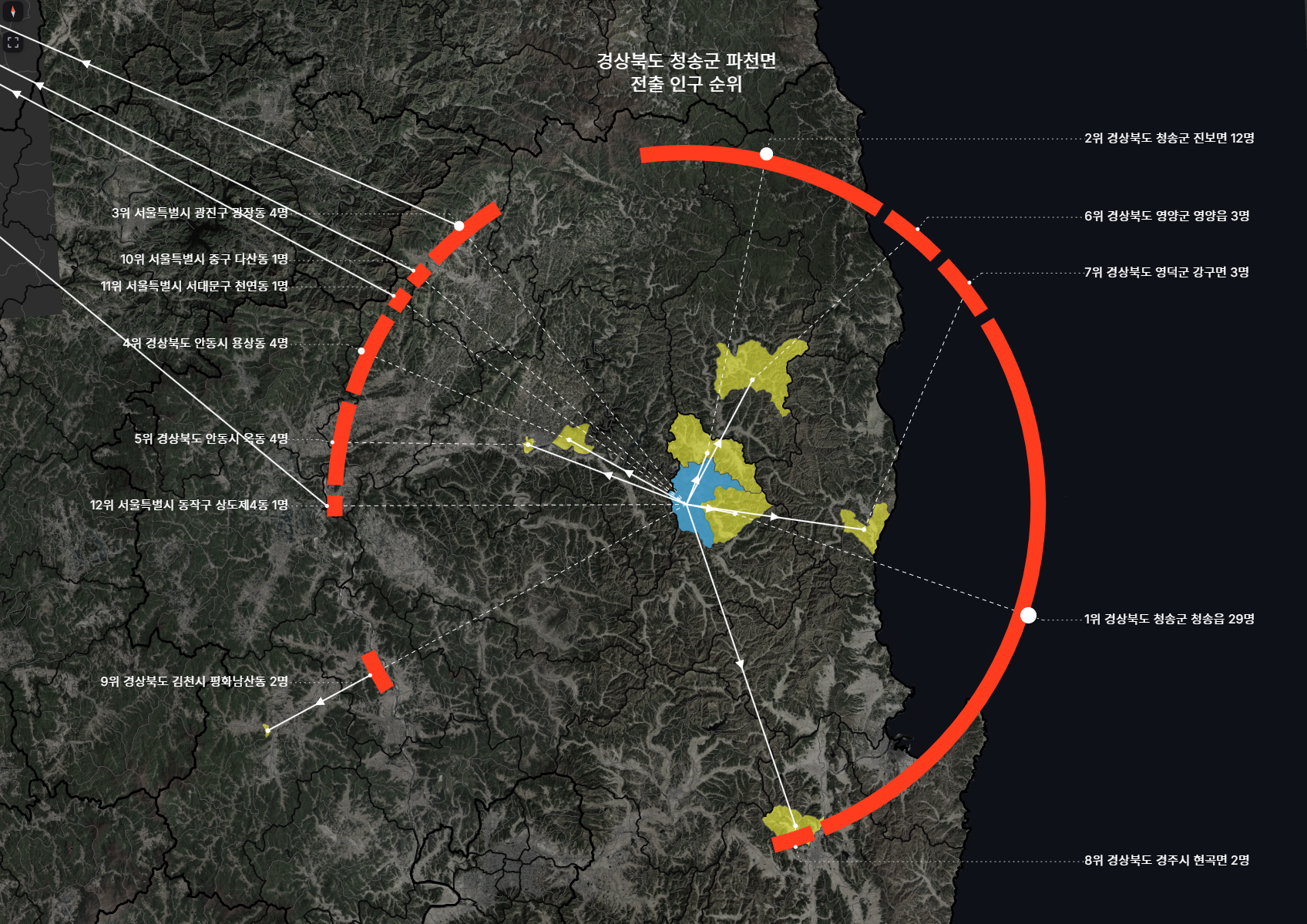
청송군 파천면
10위 안에 서울 읍면동이 네 곳 포함되었다. 그래봤자 모두 합쳐서 7명이긴 하다.
여튼, 환형의 표현에서 이동선의 간격을 한 번 벌려주니, 원래 곧바로 이었다면 출발지인 파천면에서 서울로 서로 예각을 이루는 선들이 여러개 겹쳐 보였겠지만, 방향성을 잃지 않으면서도 웬만큼 잘 구분되어 보인다.
약간 확대한 상태. 화면 안에 목적지가 모두 들어오지 않아도 괜찮다. 이미 도착지점의 이동량과 도착지 이름을 표현해주었기 때문이다.
반응은 실시간으로 나타난다. 조정 과정에서 루프를 좀 돌지만 2024년의 컴퓨터는 그런 작업을 순식간에 해치운다.
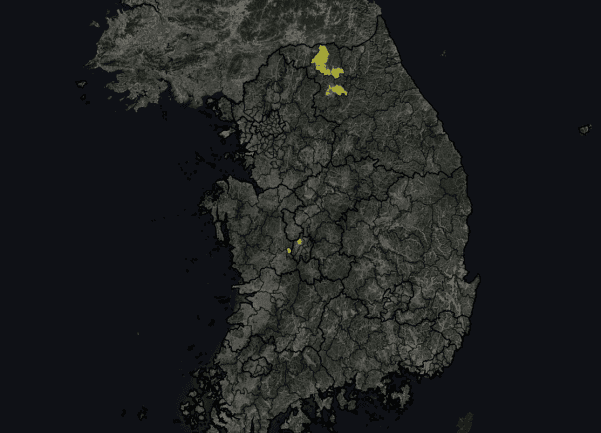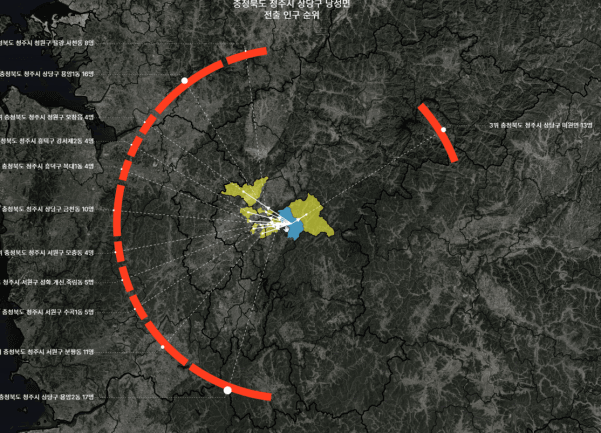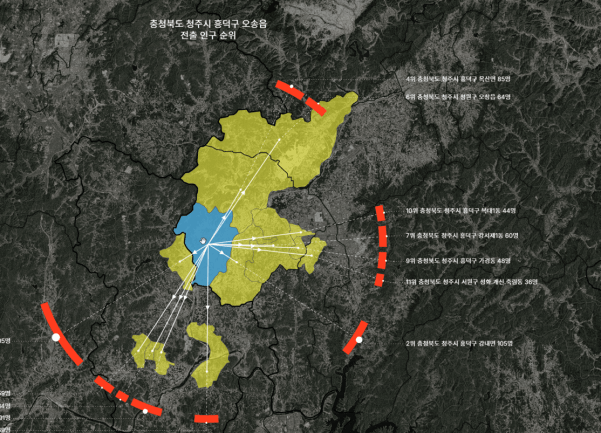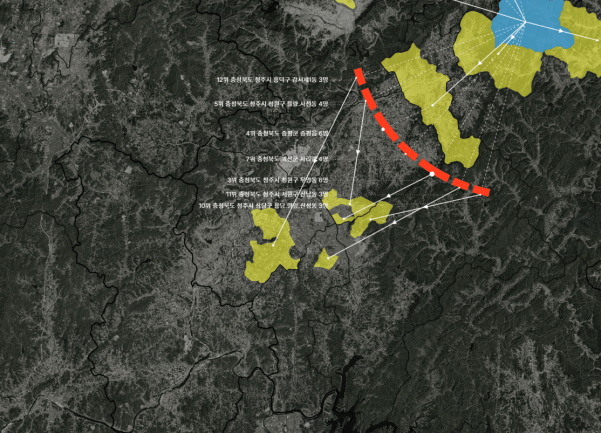
디테일은 항상 중요하다. 아래에서 축소에 따라 점선과 실선의 위계가 뒤바뀌는 경우를 볼 수 있다.
이 프로젝트가 런칭하고 난 뒤에는 인구이동 데이터를 직접 탐색할 수 있는 웹페이지를 만들어서 여기에 공개해 볼 생각이다.
'Function' 카테고리의 다른 글
| OpenStreetMap과 GTFS 데이터를 이용한 도시 자원 접근성 분석 방법 (1) | 2025.03.27 |
|---|---|
| 전세계 기온 시각화 (2) | 2024.12.02 |
| OD 시각화 5 : deck.gl.TripsLayer 의 커스터마이징 (0) | 2024.10.30 |
| deck.gl로 만든 웹 지도의 hillshade 표현 (0) | 2024.10.28 |
| 벡터 타일 3 : 웹에서 대용량 공간 데이터 시각화하기 (0) | 2024.08.11 |




